Procedure

Apparatus:

Heater, temperature-indicators, box containing metallic hemisphere with provision for water-flow through its annulus, a suitable black body which can be connected at the bottom of this metallic hemisphere.

Procedure for performing real lab

1. Remove the disc from the bottom of the hemisphere and switch on the heater and allow the water to flow through it.
2. Allow the hemisphere to reach the steady state and note down the temperature T₁, T₂, T₃ .
3. Fit the disc (black body) at the bottom of the hemisphere and note down its rise in temperature with respect to time till steady state is reached.
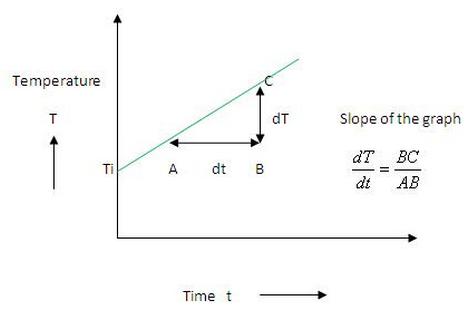
4. A graph is plotted with temperature of disc along Y-axis and time along X-axis as shown.
5. Find out the slope dT/dt from the graph.

Procedure for performing simulator

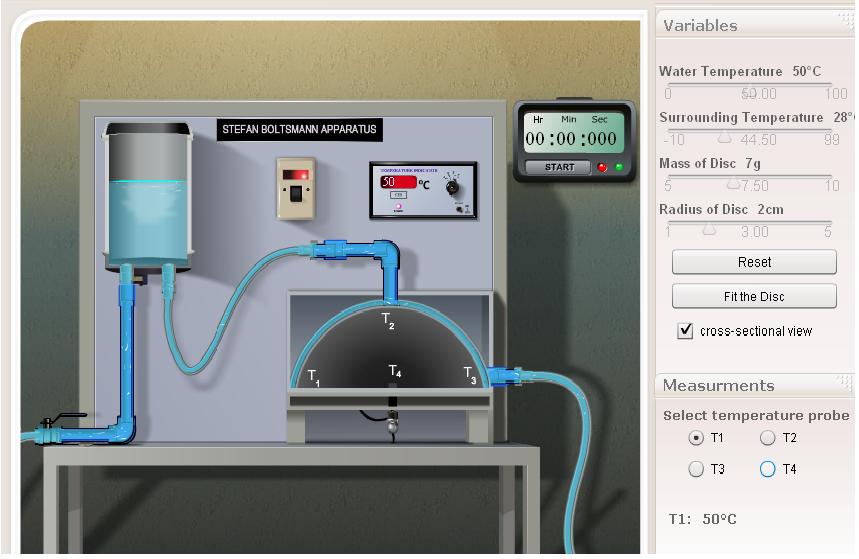
1. Choose desirable values of water temperature, surrounding temperature, mass and radius of the disc using the sliders.
2. Click the "Power ON" button and wait till T₁, T₂ ,T₃ reach steady state. Note down its values.
3. Putting T₄ button, click "Fit the disc'' option.
4. Note down T₄ at different intervals of time till it reaches steady state.
5. Plot Temperature-Time graph and determine its slope $\frac{dT}{dt}$.
6. Determine Stefan's constant $\sigma$ using the given formula.

Observations

Calculations

Mass of the copper disc = ...... $kg$

Specific heat of copper = ...... $Jkg^{-1}$

Radius of the disc = ..... $m$

Area of the disc = ......$m^{2}$

Slope of the graph $\frac{dT}{dt}$ = ............... $Ks^{-1}$

Substituting the values in the given expression,

$$\sigma =\frac{mC_{p}}{A(T_{h}^4-T_{b}^{4})}\frac{dT}{dt}$$

Result

Stefan-Boltzman's constant, $\sigma = .............. Wm^{-2}K^{-4}$